Gráficas
Las gráficas se utilizan habitualmente en cualquier tipo de publicación. Sin embargo, hay ciertos aspectos a tener en cuenta a la hora de considerarlas "buenas gráficas".
En este ejercicio he elegido un par de gráficas sobre temas en los que normalmente se presentan los datos de esta forma, como son la cantidad de contagios por coronavirus y las encuestas de intención de voto en elecciones.
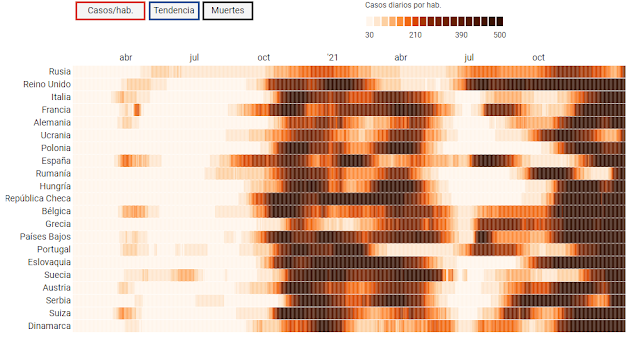
A continuación, se muestra el primer gráfico en el que se pueden ver los casos diarios de Covid-19 por habitante en diferentes países durante 2020 y 2021. En el eje Y tenemos los diferentes países europeos y en el eje X la escala temporal que se especifica cada tres meses. Emplea una escala de colores para presentar la cantidad de casos diarios por habitante, de esta forma de un vistazo se puede ver la evolución y comparar los valores entre los países.
En la escala observo dos aspectos que se deberían mejorar: por un lado, se muestran 18 tonos diferentes dando a entender que cada tono equivale a un aumento de 30 casos. Esto se cumple hasta el valor indicado de 390, ya que el último tono debería equivaler a 540 casos en vez de a 500. Por otro lado, se trata de un gráfico interactivo que he encontrado en la web del periódico, por lo que se puede seleccionar y ver la cantidad precisa en cada fecha. Este dato es importante, ya que la escala de color termina en los 500 casos y a partir de ese valor no se hace una distinción de color. Se puede comprobar que hay muchas fechas con casos muy superiores a 500 (2.600 el máximo que he encontrado encontrado). Por tanto, la escala de color no es correcta e induce a error, debido a que no cubre los valores desde el mínimo al máximo.
Por lo tanto, considero que esta gráfica a simple vista facilita información rápidamente, permite hacer comparativas entre países y ver la evolución de los casos en el tiempo, pero no comunica correctamente su mensaje; porque no muestra realmente todos los datos. Es posible que una gráfica lineal (una línea por cada país y considerando eje x - tiempo y eje y - cantidad de casos) fuera más eficaz para transmitir esta información.
Como conclusión, me gustaría añadir que cuando he estado buscando gráficas para realizar el ejercicio, he tenido serias dudas sobre si iba a encontrar gráficas con errores y si mi análisis iba a ser demasiado simple. Para mi sorpresa y después de analizarlas en detalle, algo que reconozco que no hago habitualmente, y detectar estos errores, creo que ya no voy a ver las gráficas de la misma forma.
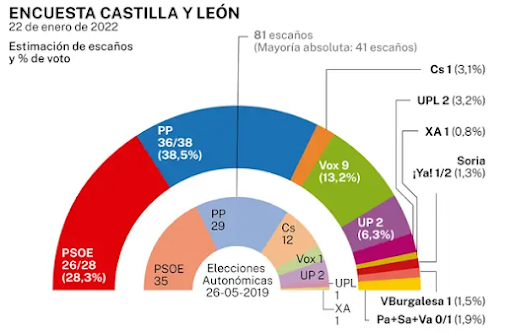
Me alegro de que hayas aprendido a mirar las gráficas con más profundidad. Hay todo un mundo en ello. Coincido bastante en tus análisis. Las gráficas "de hemiciclo" son malas desde el concepto, especialmente cuando se pretenden comparar dos poniendo una dentro de otra. La magnitud que se aprecia más diréctamente es el área (cosas de la psicología de la percepción) y eso es proporcional al ángulo, pero no entre un hemiciclo y otro. En fin, no me enrollo más aquí, pero tienes razón en que es bastante mala.
ResponderEliminar